Logaritmos

LOGARITMOS

Representación gráfica de logaritmos en varias bases:el rojo representa el logaritmo en base e,el verde corresponde a la base 10,y el purpura al de la base 1,7.Los logaritmos de todas las bases pasan por el punto (1, 0), esto es debido a que cualquier número elevado a la cero es igual a uno, y también los puntos (b, 1) para la base b, debido a que cualquier número elevado a la unidad es igual a sí mismo.
En matemáticas, el logaritmo es el exponente (o potencia) a la que un número fijo, llamado base, se ha de elevar para obtener un número dado.
Es la función inversa de la exponencial x = bn, que permite obtener n.
Esta función se escribe como: n = logb x.
Así, en la expresión 102 = 100, el logaritmo de 100 en base 10 es 2, y se escribe como log10 100 = 2.
El logaritmo es una de tres funciones relacionadas entre sí: en bn = x, puede encontrarse b con
radicales, n con logaritmos y x con esponenciación.
Se denomina logaritmo neperiano o logaritmo natural (ln) al logaritmo en base e de un número.


Historia
Joost Bürgi, un matemático y relojero suizo al servicio del duque de Hesse-Kassel, concibió por vez primera los logaritmos. El método de logaritmos naturales fue propuesto inicialmente en 1614, en un libro intitulado Mirifici Logarithmorum Canonis Descriptio, escrito por John Napier (latinizado Neperus), Barón de Merchiston en Escocia, que nació cerca de1550, y murió en 1617, cuatro años después de la publicación de su memorable invención.
Este método contribuyó al avance de la ciencia, y especialmente de la astronomía, facilitando la realización de cálculos muy complejos. Antes del advenimiento de las calculadoras y computadoras, era constantemente usado en estadística, navegación, y otras ramas de la matemática aplicada. Además de su utilidad en el cómputo, los logaritmos también ocuparon un importante lugar en las matemáticas más avanzadas.


Uso de logaritmos
La función logb(x) = a está definida donde quiera que x es un número real positivo y b es un número real positivo diferente a 1. Véase identidades logarítmicas para diversas reglas relacionadas a las funciones logarítmicas. También es posible definir logaritmos para argumentos
complejos.
Para enteros b y x, el número logb(x) es irracional (no puede representarse como el cociente de dos enteros) si b o x tiene un factor primo que el otro no tiene.

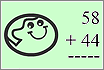Mathematics
¿Eres bueno sumando y restando cifras? demuéstralo en este juego de matemáticas. Elige el resultado antes de que se acabe el tiempo

La descongelación de Fry

Fry se congeló el 1 de Enero de 2000 a las 0:00 AM. A partir de entonces, empezó una cuenta atrás de 1000 años para la descongelación. El problema es que existen distintos tipos de años (trópico, sideral, juliano, gregoriano...), cada uno con una duración particular determinada. El más "lógico" para usar es el "año gregoriano" medio, que tiene 365.2425 días y es por el que se rigen los calendarios actuales (que se llaman precisamente calendarios gregorianos). Por lo tanto, 1000 años son 365242.5 días. Entonces Fry se descongelaría el 31 de Diciembre de 2999 a las 12 del mediodía (teniendo en cuenta los años bisiestos y todo eso).
Efectivamente, Fry se descongela el 31 de Diciembre de 2999 y, aunque no queda explícitamente indicada la hora, todo parece indicar que ocurre hacia el mediodía.

Add like mad

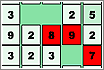
Add Like Mad
Haz click sobre los cuadrados y suma los números que te indican en la parte inferior del juego. Intenta deshacerte de todos los cuadrados de cada nivel

Sombrero Samuray de papel

Para aprender a construir un sombrero de los samurais con papel

Crear sombrero Samuray

Para realizar esta manualidad se ha de disponer de una hoja de papel (o cartulina) cuadrada.

Doblar diagonalmente la hoja cuadrada de papel...

...de este modo se obtendrá un doble triángulo, que se doblará de nuevo a lo largo de las líneas de trazos que unen los puntos medios de los catetos con el de la hipotenusa.

Ahora la estructura tiene una forma cuadrada (1cuarto del tamaño inicial), constituye la base del sombrero del samurai.
Se levantan las aletas doblándolas a lo largo de la diagonal -línea de trazos- uniendo los dos vértices con el de arriba.

Doblar de nuevo a lo largo de las dos líneas de trazos.

Doblar la primera ala de la parte inferior (dejando unos centímetros de la diagonal del cuadrado) -siguiendo la línea de trazos- hacia el vértice superior.

Una vez levantada el ala -como se puede ver en la figura- doblarla a lo largo de la línea que se sobrepone a la diagonal

Doblar la ala que queda hacia el otro lado, de manera que el vértice de dicha ala se coloque sobre el vértice superior del sombrero.
Apretar todos los lados del sombrero para marcar las líneas.

El sombrero de samurai también se denomina kabuto.

Papiroflexia y Matemáticas

No me resultaba difícil últimamente encontrarme con alguna composición, a partir de módulos, en la que se hallaran representados los tres planos del espacio. No obstante, la imagen ideal que yo podía tener de cómo representarlos no se ajustaba a lo que me iba encontrando.

Es por ello que me planteé el reto de realizar una composición modular con los tres planos cruzándose en el espacio y que estuvieran inscritos en un hexaedro. Me impuse también otros criterios como el de jugar con un color para cada plano, que los módulos fueran los menos posibles, que encastraran firmemente y que, por ende, resultaran relativamente fáciles de confeccionar.

Lo primero que me planteé fue la manera de reducir al mínimo los módulos. Sin pensármelo mucho, me puse –literalmente– manos a la obra: cogí seis papeles cuadrados, los doblé por la mitad formando rectángulos y me hice la composición sobre la marcha. Bien, aquello parecía que marchaba: los seis rectángulos podían entrecruzarse formando la composición que yo buscaba y ahora sólo me faltaba buscar la manera de hacerlos encastrar unos con los otros. ¡Necesitaba unos bolsillos en aquellos rectángulos y unas puntas que pudieran meterse en dichos bolsillos, pero cómo!

La verdad es que los que practicamos la papiroflexia de manera asidua tenemos una ventaja: muchas veces las soluciones nos vienen dadas por otras figuras, que en la inmensa mayoría de las veces no tienen nada que ver con lo que pretendemos. Así fue como, casi como un acto reflejo, tras plantearme el cómo sacar bolsillos y puntas, me vino de primeras a la cabeza una composición infantil tradicional: ¡el catamarán o barco doble! Aquella figura tenía todo lo que yo estaba buscando, y además en los lugares idóneos.

Al llevarlo a la práctica tuve un pequeño contratiempo: si hacía los plegados de la manera más perfecta que me fuera posible, tenía auténticos problemas de encaje, fundamentalemnte con los últimos módulos. Por un lado, el grosor del papel que se me acumulaba en el centro de los tres planos me impedía introducir las pestañas de estos últimos módulos en sus bolsillos correspondientes; y por otro, la ortogonalidad de los planos me dificultaba enormente encastrarlos.

Por tanto, y como consejo: Prestad atención al grosor del papel y, en función de ello, plegad en el paso número 2 con la suficiente “imperfección” que permita la holgura necesaria entre los bolsillos y el módulo (con sus pestañas) que se interpondrá entre ellos.

Suerte y que disfrutéis.

Página:
http://divulgamat.ehu.es/weborriak/Cultura/papiroflexia/index.asp